Introduction
In the study of logic, mathematics, and computer science, the concept of a truth table is fundamental. If you’ve ever wondered what is a truth table in logic, you’re not alone. Truth tables are essential tools used to analyze and visualize logical expressions and propositions by displaying all possible truth values of their components.
This article will thoroughly explain what a truth table is, its importance in logic, the key logical operators involved, and how to construct one effectively. Whether you’re a student, programmer, or logic enthusiast, this guide will provide a solid foundation.
What Is a Truth Table in Logic?
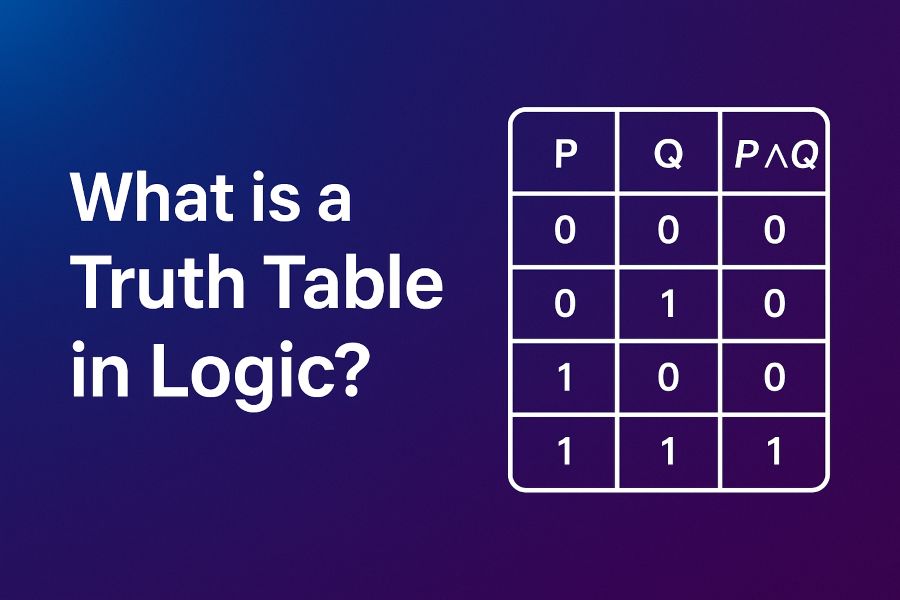
A truth table in logic is a systematic tabular representation used to display all possible combinations of truth values for a set of logical variables, alongside the resulting truth value of a logical expression. It helps illustrate how the truth or falsity of complex statements depends on their individual components.
By using truth tables, one can evaluate the validity of arguments, check equivalences, and better understand logical operations.
Why Are Truth Tables Important in Logic?
- Analyze Logical Expressions: Truth tables clarify how different inputs affect the outcome.
- Verify Logical Equivalences: Help determine if two expressions always have the same truth value.
- Support Mathematical Proofs: Assist in validating logical arguments rigorously.
- Foundation for Computer Science: Crucial for designing circuits, writing algorithms, and understanding computation.
- Teach Logical Reasoning: Widely used in philosophy and critical thinking education.
Key Components of a Truth Table in Logic
- Logical Variables: These are the basic propositions or statements which can be true (T) or false (F).
- Logical Operators: Symbols that combine or modify variables to form expressions (AND, OR, NOT, etc.).
- Rows: Each row represents one possible combination of truth values for the variables.
- Columns: Columns correspond to variables, sub-expressions, and the overall expression being analyzed.
- Truth Values: Each cell contains T (true) or F (false), showing the evaluation result.
Common Logical Operators Used in Truth Tables
Understanding these operators is key to interpreting truth tables:
- AND ( ∧ ): True if both operands are true; otherwise false.
- OR ( ∨ ): True if at least one operand is true.
- NOT ( ¬ ): Negates or inverts the truth value.
- IMPLICATION ( → ): False only when the first operand is true and the second is false.
- BICONDITIONAL ( ↔ ): True when both operands have the same truth value.
How Does a Truth Table Work?
Truth tables enumerate every possible combination of truth values for the variables involved. By evaluating the logical operators step-by-step, the table shows the outcome of the expression under each scenario.
For example, if you have two variables AAA and BBB, each can be either true or false. The truth table lists all four possible combinations (TT, TF, FT, FF), then calculates the result of the expression for each.
Step-by-Step Guide to Construct a Truth Table in Logic
Step 1: Identify Variables
Determine all unique variables within your logical statement. For example, AAA, BBB, and CCC.
Step 2: Calculate Number of Rows
Use the formula 2n2^n2n, where nnn is the number of variables. For 3 variables, you will have 8 rows.
Step 3: List Truth Value Combinations
Create columns for each variable and list all possible truth value combinations in binary order.
| A | B | C |
|---|---|---|
| T | T | T |
| T | T | F |
| T | F | T |
| T | F | F |
| F | T | T |
| F | T | F |
| F | F | T |
| F | F | F |
Step 4: Break Expression Into Sub-Expressions
Divide the logical expression into simpler parts for evaluation and add columns for each.
Step 5: Evaluate Sub-Expressions Row by Row
Apply logical operator rules to calculate truth values for each sub-expression.
Step 6: Calculate the Final Column
Combine sub-expressions to determine the truth value of the entire expression for each row.
Example: What Is a Truth Table in Logic for (A∧B)→C(A \land B) \to C(A∧B)→C?
| A | B | C | A∧BA \land BA∧B | (A∧B)→C(A \land B) \to C(A∧B)→C |
|---|---|---|---|---|
| T | T | T | T | T |
| T | T | F | T | F |
| T | F | T | F | T |
| T | F | F | F | T |
| F | T | T | F | T |
| F | T | F | F | T |
| F | F | T | F | T |
| F | F | F | F | T |
Applications of Truth Tables in Logic
- Validating Arguments: Confirming if a logical argument is valid or not.
- Simplifying Expressions: Aiding in Boolean algebra and digital logic design.
- Programming: Understanding conditional logic and control flow.
- Philosophy: Analyzing the soundness of logical propositions.
- Mathematics: Proving equivalences and theorems.
Advantages of Using Truth Tables
- Clarity: Visually represent complex logical relationships.
- Systematic: Leave no combination unexplored.
- Accuracy: Minimize errors in logical analysis.
- Universal: Applicable across various disciplines.
Common Mistakes When Working With Truth Tables
- Forgetting to list all possible truth value combinations.
- Misinterpreting logical operator precedence.
- Confusing the meaning of implication and biconditional operators.
- Skipping intermediate steps in complex expressions.
Tools to Create Truth Tables Easily
Manually creating truth tables can be tedious for expressions with many variables. Online truth table generators provide quick, accurate results. TruthTableGenerator.io is a secure, anonymous, and free tool that instantly builds truth tables for your logic expressions without requiring login.
Conclusion
Understanding what is a truth table in logic is crucial for anyone interested in logic, computing, or mathematics. Truth tables provide a clear, systematic method to analyze and verify logical expressions. By mastering how to construct and interpret truth tables, you can enhance your logical reasoning and problem-solving skills. Whether you’re learning Boolean algebra or designing circuits, truth tables are indispensable.
For quick and reliable truth table generation, consider using trusted online tools like TruthTableGenerator.io, offering an anonymous and user-friendly experience.
Frequently Asked Questions (FAQs)
What does a truth table represent in logic?
It represents all possible truth values of logical variables and the output of a logical expression for those values.
Can truth tables handle complex expressions?
Yes, by breaking expressions into sub-expressions, truth tables can analyze complex logic systematically.
Why is the number of rows in a truth table 2n2^n2n?
Because each variable can be true or false, so for nnn variables, there are 2n2^n2n possible combinations.